Efficient Frontier Workflow Notebook - Execution Ready¶
Workflow Notebook¶
This is a compact notebook for headless execution. Supporting notebooks with exploratory notes is here
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import quandl
import scipy.optimize as sco
plt.style.use('fivethirtyeight')
np.random.seed(777)
%matplotlib inline
%config InlineBackend.figure_format = 'retina'quandl.ApiConfig.api_key = 'zCYyKsBbzk94ye5yRjvs'
stocks = ['AAPL','AMZN','GOOGL','FB']
data = quandl.get_table('WIKI/PRICES', ticker = stocks,
qopts = { 'columns': ['date', 'ticker', 'adj_close'] },
date = { 'gte': '2016-1-1', 'lte': '2017-12-31' }, paginate=True)
data.head()Loading...
df = data.set_index('date')
df.head()Loading...
table = df.pivot(columns='ticker')
# By specifying col[1] in below list comprehension
# You can select the stock names under multi-level column
table.columns = [col[1] for col in table.columns]
table.head(10)Loading...
plt.figure(figsize=(14, 7))
for c in table.columns.values:
plt.plot(table.index, table[c], lw=3, alpha=0.8,label=c)
plt.legend(loc='upper left', fontsize=12)
plt.ylabel('price in $')Text(0, 0.5, 'price in $')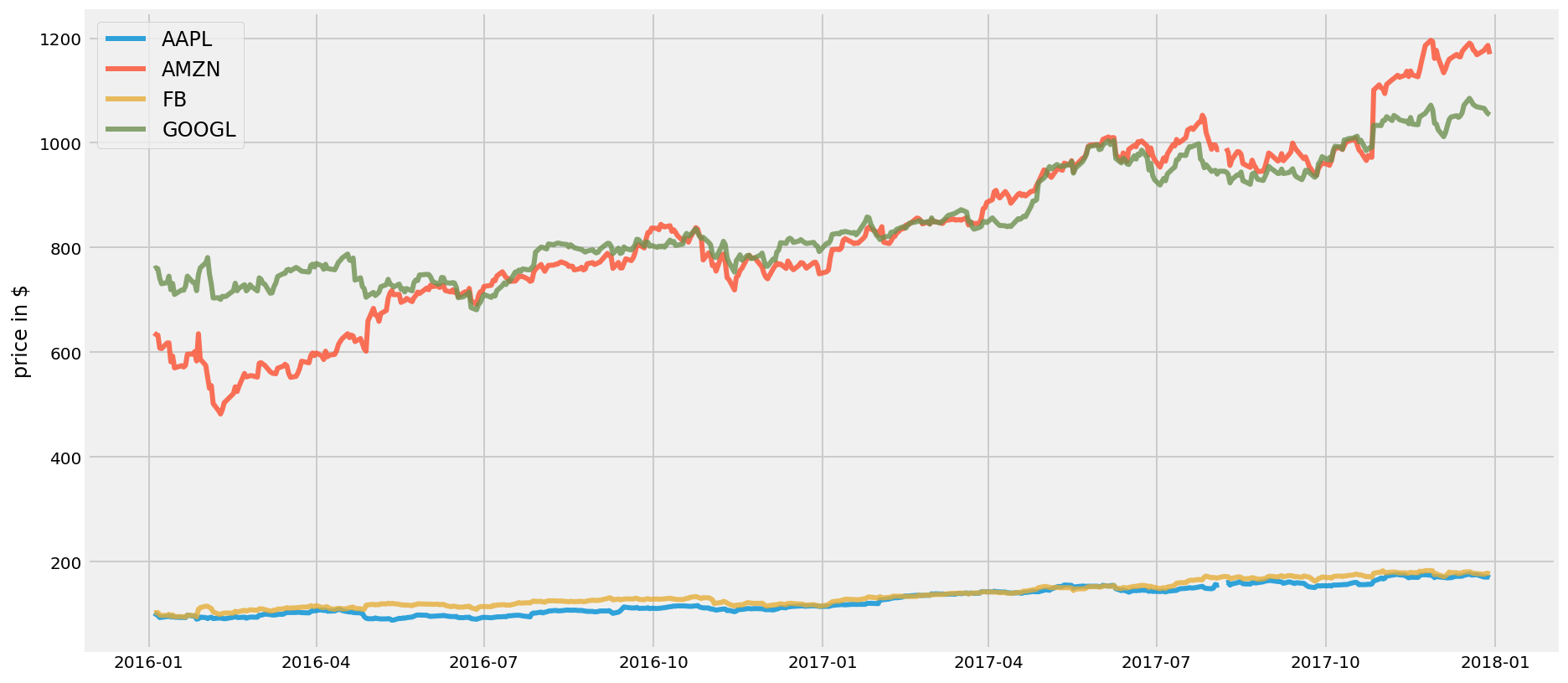
returns = table.pct_change()
plt.figure(figsize=(14, 7))
for c in returns.columns.values:
plt.plot(returns.index, returns[c], lw=3, alpha=0.8,label=c)
plt.legend(loc='upper right', fontsize=12)
plt.ylabel('daily returns')Text(0, 0.5, 'daily returns')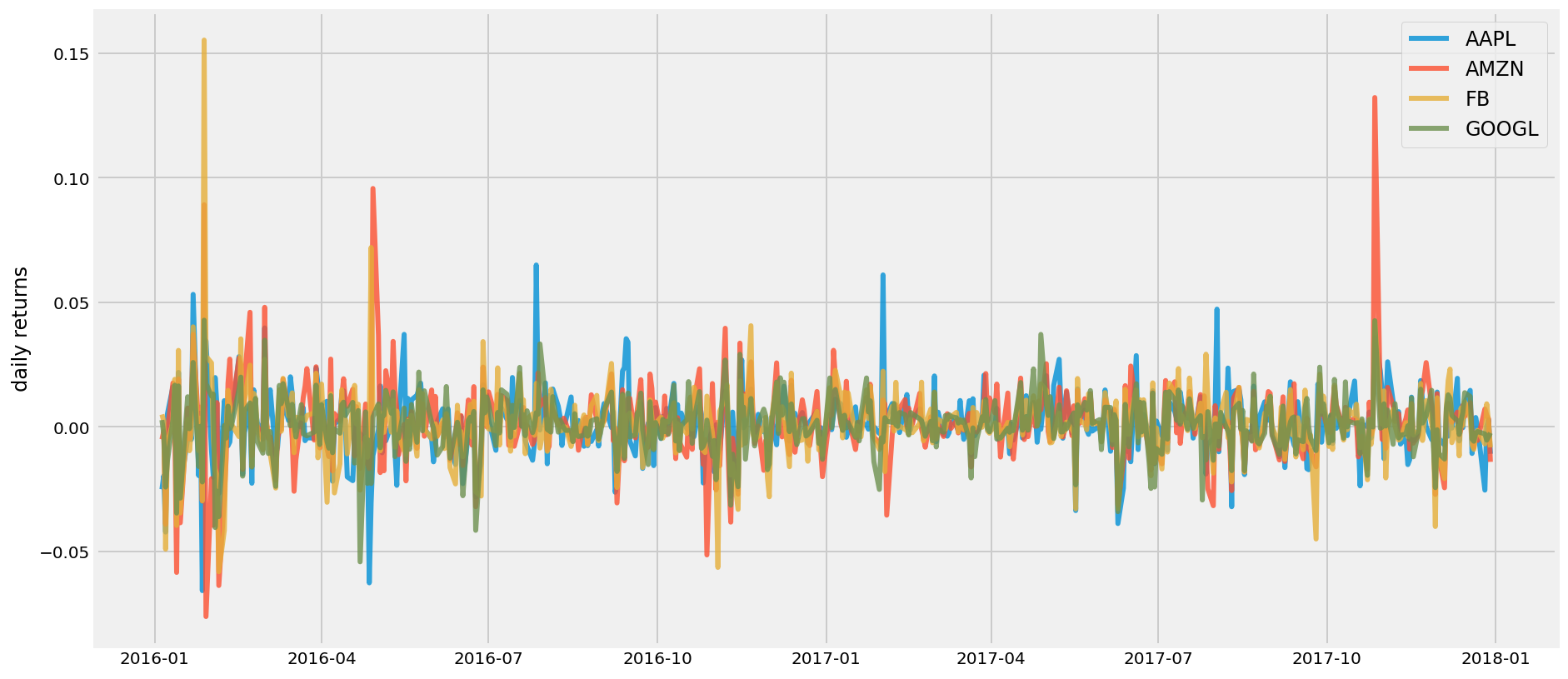
def portfolio_annualised_performance(weights, mean_returns, cov_matrix):
returns = np.sum(mean_returns*weights ) *252
std = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights))) * np.sqrt(252)
return std, returnsdef random_portfolios(num_portfolios, mean_returns, cov_matrix, risk_free_rate):
results = np.zeros((3,num_portfolios))
weights_record = []
for i in range(num_portfolios):
weights = np.random.random(4)
weights /= np.sum(weights)
weights_record.append(weights)
portfolio_std_dev, portfolio_return = portfolio_annualised_performance(weights, mean_returns, cov_matrix)
results[0,i] = portfolio_std_dev
results[1,i] = portfolio_return
results[2,i] = (portfolio_return - risk_free_rate) / portfolio_std_dev
return results, weights_recordreturns = table.pct_change()
mean_returns = returns.mean()
cov_matrix = returns.cov()
num_portfolios = 25000
risk_free_rate = 0.0178mean_returns.plot.barh()<AxesSubplot:>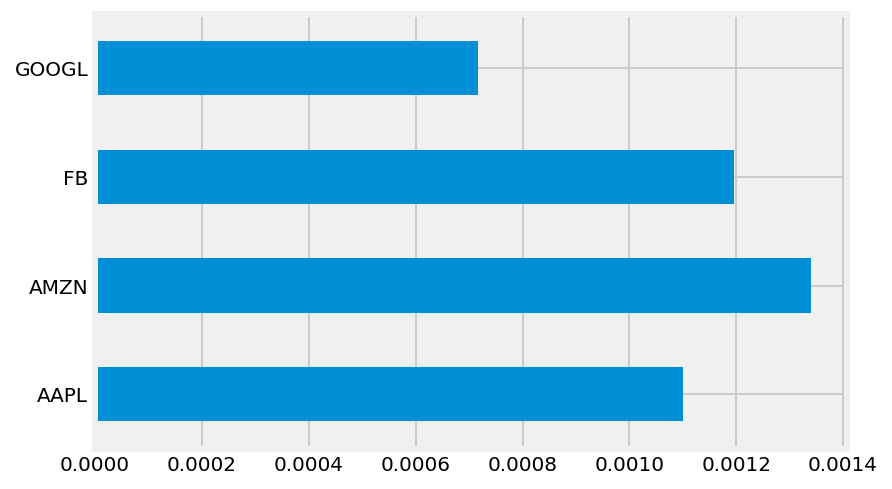
cov_matrixLoading...
def neg_sharpe_ratio(weights, mean_returns, cov_matrix, risk_free_rate):
p_var, p_ret = portfolio_annualised_performance(weights, mean_returns, cov_matrix)
return -(p_ret - risk_free_rate) / p_var
def max_sharpe_ratio(mean_returns, cov_matrix, risk_free_rate):
num_assets = len(mean_returns)
args = (mean_returns, cov_matrix, risk_free_rate)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bound = (0.0,1.0)
bounds = tuple(bound for asset in range(num_assets))
result = sco.minimize(neg_sharpe_ratio, num_assets*[1./num_assets,], args=args,
method='SLSQP', bounds=bounds, constraints=constraints)
return resultdef portfolio_volatility(weights, mean_returns, cov_matrix):
return portfolio_annualised_performance(weights, mean_returns, cov_matrix)[0]
def min_variance(mean_returns, cov_matrix):
num_assets = len(mean_returns)
args = (mean_returns, cov_matrix)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bound = (0.0,1.0)
bounds = tuple(bound for asset in range(num_assets))
result = sco.minimize(portfolio_volatility, num_assets*[1./num_assets,], args=args,
method='SLSQP', bounds=bounds, constraints=constraints)
return resultdef efficient_return(mean_returns, cov_matrix, target):
num_assets = len(mean_returns)
args = (mean_returns, cov_matrix)
def portfolio_return(weights):
return portfolio_annualised_performance(weights, mean_returns, cov_matrix)[1]
constraints = ({'type': 'eq', 'fun': lambda x: portfolio_return(x) - target},
{'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bounds = tuple((0,1) for asset in range(num_assets))
result = sco.minimize(portfolio_volatility, num_assets*[1./num_assets,], args=args, method='SLSQP', bounds=bounds, constraints=constraints)
return result
def efficient_frontier(mean_returns, cov_matrix, returns_range):
efficients = []
for ret in returns_range:
efficients.append(efficient_return(mean_returns, cov_matrix, ret))
return efficientsdef display_calculated_ef_with_random(mean_returns, cov_matrix, num_portfolios, risk_free_rate):
results, _ = random_portfolios(num_portfolios,mean_returns, cov_matrix, risk_free_rate)
max_sharpe = max_sharpe_ratio(mean_returns, cov_matrix, risk_free_rate)
sdp, rp = portfolio_annualised_performance(max_sharpe['x'], mean_returns, cov_matrix)
max_sharpe_allocation = pd.DataFrame(max_sharpe.x,index=table.columns,columns=['allocation'])
max_sharpe_allocation.allocation = [round(i*100,2)for i in max_sharpe_allocation.allocation]
max_sharpe_allocation = max_sharpe_allocation.T
max_sharpe_allocation
min_vol = min_variance(mean_returns, cov_matrix)
sdp_min, rp_min = portfolio_annualised_performance(min_vol['x'], mean_returns, cov_matrix)
min_vol_allocation = pd.DataFrame(min_vol.x,index=table.columns,columns=['allocation'])
min_vol_allocation.allocation = [round(i*100,2)for i in min_vol_allocation.allocation]
min_vol_allocation = min_vol_allocation.T
print("-"*80)
print("Maximum Sharpe Ratio Portfolio Allocation\n")
print("Annualised Return:", round(rp,2))
print("Annualised Volatility:", round(sdp,2))
print("\n")
print(max_sharpe_allocation)
print("-"*80)
print("Minimum Volatility Portfolio Allocation\n")
print("Annualised Return:", round(rp_min,2))
print("Annualised Volatility:", round(sdp_min,2))
print("\n")
print(min_vol_allocation)
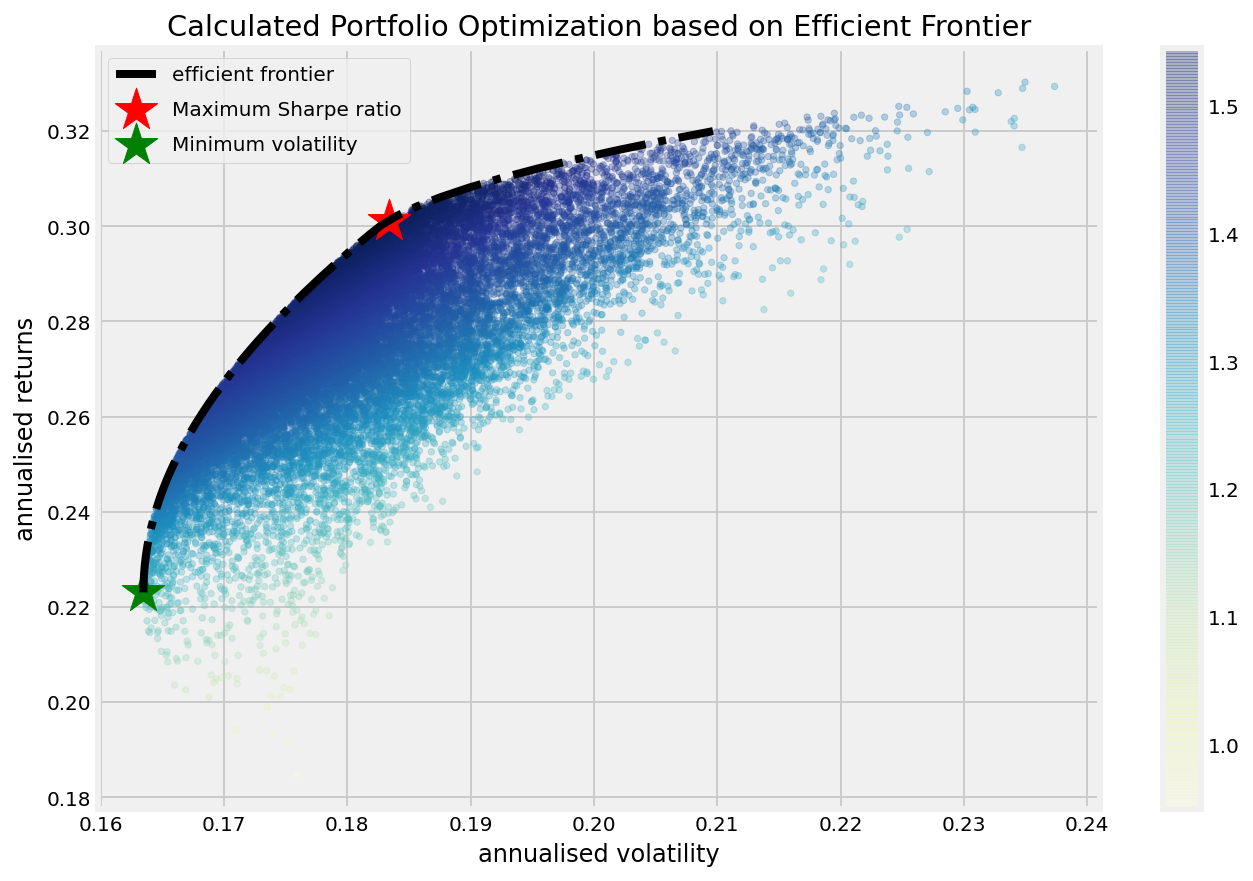
plt.figure(figsize=(10, 7))
plt.scatter(results[0,:],results[1,:],c=results[2,:],cmap='YlGnBu', marker='o', s=10, alpha=0.3)
plt.colorbar()
plt.scatter(sdp,rp,marker='*',color='r',s=500, label='Maximum Sharpe ratio')
plt.scatter(sdp_min,rp_min,marker='*',color='g',s=500, label='Minimum volatility')
target = np.linspace(rp_min, 0.32, 50)
efficient_portfolios = efficient_frontier(mean_returns, cov_matrix, target)
plt.plot([p['fun'] for p in efficient_portfolios], target, linestyle='-.', color='black', label='efficient frontier')
plt.title('Calculated Portfolio Optimization based on Efficient Frontier')
plt.xlabel('annualised volatility')
plt.ylabel('annualised returns')
plt.legend(labelspacing=0.8)display_calculated_ef_with_random(mean_returns, cov_matrix, num_portfolios, risk_free_rate)--------------------------------------------------------------------------------
Maximum Sharpe Ratio Portfolio Allocation
Annualised Return: 0.3
Annualised Volatility: 0.18
AAPL AMZN FB GOOGL
allocation 44.67 29.05 26.28 0.0
--------------------------------------------------------------------------------
Minimum Volatility Portfolio Allocation
Annualised Return: 0.22
Annualised Volatility: 0.16
AAPL AMZN FB GOOGL
allocation 34.02 0.73 6.98 58.26
def display_ef_with_selected(mean_returns, cov_matrix, risk_free_rate):
max_sharpe = max_sharpe_ratio(mean_returns, cov_matrix, risk_free_rate)
sdp, rp = portfolio_annualised_performance(max_sharpe['x'], mean_returns, cov_matrix)
max_sharpe_allocation = pd.DataFrame(max_sharpe.x,index=table.columns,columns=['allocation'])
max_sharpe_allocation.allocation = [round(i*100,2)for i in max_sharpe_allocation.allocation]
max_sharpe_allocation = max_sharpe_allocation.T
max_sharpe_allocation
min_vol = min_variance(mean_returns, cov_matrix)
sdp_min, rp_min = portfolio_annualised_performance(min_vol['x'], mean_returns, cov_matrix)
min_vol_allocation = pd.DataFrame(min_vol.x,index=table.columns,columns=['allocation'])
min_vol_allocation.allocation = [round(i*100,2)for i in min_vol_allocation.allocation]
min_vol_allocation = min_vol_allocation.T
an_vol = np.std(returns) * np.sqrt(252)
an_rt = mean_returns * 252
print("-"*80)
print("Maximum Sharpe Ratio Portfolio Allocation\n")
print("Annualised Return:", round(rp,2))
print("Annualised Volatility:", round(sdp,2))
print("\n")
print(max_sharpe_allocation)
print("-"*80)
print("Minimum Volatility Portfolio Allocation\n")
print("Annualised Return:", round(rp_min,2))
print("Annualised Volatility:", round(sdp_min,2))
print("\n")
print(min_vol_allocation)
print("-"*80)
print("Individual Stock Returns and Volatility\n")
for i, txt in enumerate(table.columns):
print(txt,":","annuaised return",round(an_rt[i],2),", annualised volatility:",round(an_vol[i],2))
print("-"*80)
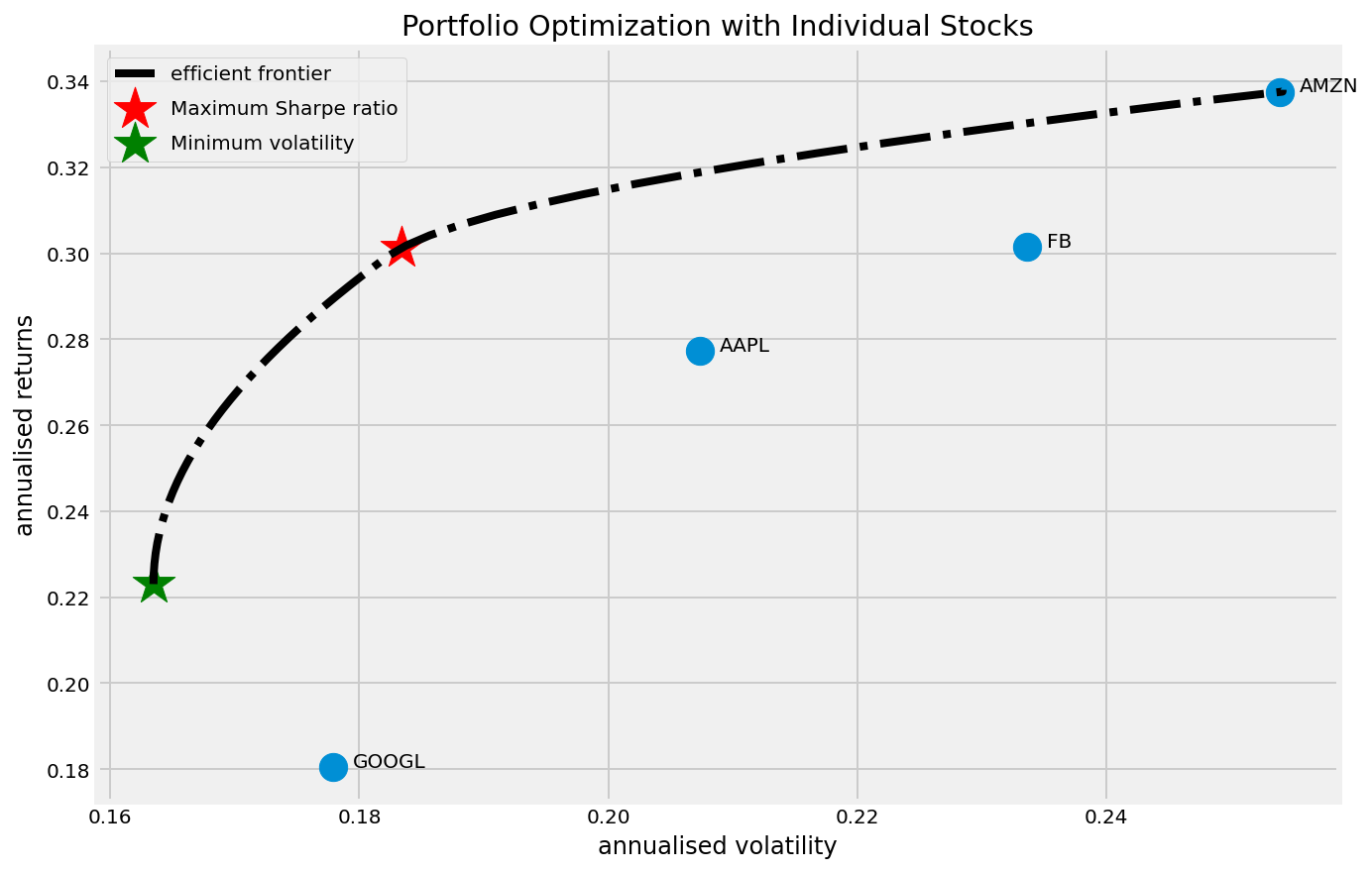
fig, ax = plt.subplots(figsize=(10, 7))
ax.scatter(an_vol,an_rt,marker='o',s=200)
for i, txt in enumerate(table.columns):
ax.annotate(txt, (an_vol[i],an_rt[i]), xytext=(10,0), textcoords='offset points')
ax.scatter(sdp,rp,marker='*',color='r',s=500, label='Maximum Sharpe ratio')
ax.scatter(sdp_min,rp_min,marker='*',color='g',s=500, label='Minimum volatility')
target = np.linspace(rp_min, 0.34, 50)
efficient_portfolios = efficient_frontier(mean_returns, cov_matrix, target)
ax.plot([p['fun'] for p in efficient_portfolios], target, linestyle='-.', color='black', label='efficient frontier')
ax.set_title('Portfolio Optimization with Individual Stocks')
ax.set_xlabel('annualised volatility')
ax.set_ylabel('annualised returns')
ax.legend(labelspacing=0.8)display_ef_with_selected(mean_returns, cov_matrix, risk_free_rate)--------------------------------------------------------------------------------
Maximum Sharpe Ratio Portfolio Allocation
Annualised Return: 0.3
Annualised Volatility: 0.18
AAPL AMZN FB GOOGL
allocation 44.67 29.05 26.28 0.0
--------------------------------------------------------------------------------
Minimum Volatility Portfolio Allocation
Annualised Return: 0.22
Annualised Volatility: 0.16
AAPL AMZN FB GOOGL
allocation 34.02 0.73 6.98 58.26
--------------------------------------------------------------------------------
Individual Stock Returns and Volatility
AAPL : annuaised return 0.28 , annualised volatility: 0.21
AMZN : annuaised return 0.34 , annualised volatility: 0.25
FB : annuaised return 0.3 , annualised volatility: 0.23
GOOGL : annuaised return 0.18 , annualised volatility: 0.18
--------------------------------------------------------------------------------